СОРОКИНА Т.П., СОРОКІН Б.П. та ін. Фізика ТЕМА 2.1.

1. МОДУЛЬ 2. Молекулярна фізика і термодинаміка 2.1.1. Молекулярно-кінетична теорія 2.1.2. Стан...
2. 2.1.2. Стан системи. Внутрішня енергія. Рівноважні і нерівноважні стану газу
3. 2.1.3. Перший початок термодинаміки
4. 2.1.4. Робота, що здійснюється тілом при зміні його об'єму
5. 2.1.5. температура
6. 2.1.6. Рівняння стану ідеального газу. Експериментальні газові закони.
7. 2.1.7. рівняння кінетичної теорії газів для тиску
8. 2.1.8. равнораспределенія енергії за ступенями свободи
9. 2.1.9. Внутрішня енергія і теплоємність ідеального газу
10. 2.1.10. Рівняння адіабати ідеального газу
11. 2.1.11. политропического процеси
12. 2.1.12. барометрична формула
13. 2.1.13. РозподілБольцмана

МОДУЛЬ 2. Молекулярна фізика і термодинаміка

2.1.1. Молекулярно-кінетична теорія

2.1.2. Стан системи. Внутрішня енергія. Рівноважні і нерівноважні стану газу

2.1.3. Перший початок термодинаміки

2.1.4. Робота, що здійснюється тілом при зміні його об'єму

2.1.5. температура

2.1.6. Рівняння стану ідеального газу. Експериментальні газові закони

2.1.7. Рівняння кінетичної теорії газів для тиску

2.1.8. Равнораспределенія енергії за ступенями свободи

2.1.9. Внутрішня енергія і теплоємність ідеального газу

2.1.10. Рівняння адіабати ідеального газу

2.1.11. политропического процеси

2.1.12. барометрична формула

2.1.13. РозподілБольцмана

2.1.1. Молекулярно-кінетична теорія

Згідно молекулярно-кінетичних уявлень, тіло в будь-якому агрегатному стані складається з великого числа малих відокремлених частинок - молекул. Молекули всякого речовини знаходяться в безладному хаотичному русі, інтенсивність якого залежить від температури. Безпосереднім доказом існування хаотичного руху молекул служить броунівський рух: під мікроскопом можна спостерігати, що малі зважені в рідині частинки завжди безладно рухаються, піддаючись ударам молекул рідини.

Для характеристики мас атомів і молекул застосовують такі величини, як атомна маса А (цю величину називають також масовим числом) і молекулярна маса М. Атомної масою А хімічного елемента називають відношення маси атома цього елемента до 1/12 маси атома С12. 1/12 маси атома С12, виражена в кілограмах, позначається Mед. Тоді маса атома (в кілограмах) дорівнює Аmед, маса молекули - Мmед.

Якщо взяти прості хімічні речовини в таких кількостях, що виконується відношення:

Досвідченим числом знайдено, що NA = 6,023 · +1026 кмоль-1. Знаючи число Авогадро, можна знайти одиничну масу: 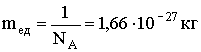Тому маса будь-якого атома дорівнює: 1,66 · 10-27А кг, маса будь-молекули дорівнює: 1,66 · 10-27М кг.

Зробимо оцінку розмірів молекул. У рідинах молекули розташовуються досить близько один до одного. Тому наближену оцінку обсягу однієї молекули можна зробити, розділивши обсяг кіломоля будь-якої рідини, наприклад, води, на число молекул в кіломоле (NA). Кіломоль (тобто 18 кг) води займає обсяг 0,018 м & sup3. Отже, на одну молекулу доводиться обсяг, рівний .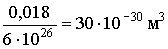

Звідси випливає, що лінійні розміри молекули води приблизно рівні .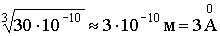

2.1.2. Стан системи. Внутрішня енергія.
Рівноважні і нерівноважні стану газу

Системою тел називається сукупність розглянутих тел. Будь-яка система може перебувати в різних станах, що відрізняються температурою, тиском, об'ємом і т.п. Подібні величини, що характеризують стан системи, називаються параметрами стану.

Не завжди будь-якої параметр має певне значення. Якщо, наприклад, температура неоднакова в різних точках тіла, то тілу не можна приписати певне значення параметра Т. В цьому випадку стан системи буде нерівновагим. Якщо таке тіло ізолювати і надати самому собі, то температура вирівняється і прийме однакове для всіх точок значення Т, і тіло перейде в рівноважний стан. Це значення Т не зміниться до тих пір, поки тіло не буде виведено з рівноважного стану впливом ззовні.

Рівноважним станом системи називається такий стан, при якому всі параметри системи мають певні значення, що залишаються постійними як завгодно довго при незмінних зовнішніх умовах.

Всякий рівноважний процес може бути представлений у вигляді графіка, причому будь-рівноважний стан зображується точкою, наприклад точка 1 (Рис. 2.1.1).

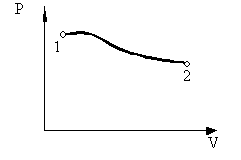
Мал. 2.1.1. Рівноважний стан системи

Всякий процес, тобто перехід системи з одного стану в інший, пов'язаний з порушенням рівноваги системи. Отже, при протіканні в системі будь-якого процесу вона проходить через послідовність нерівноважних станів. Якщо, проте, порушення рівноваги відбувається дуже повільно, то рівновага порушується незначно. Отже, в такому випадку стан системи в кожен момент часу є рівноважним, і нескінченно повільний процес буде складатися з безперервної послідовності рівноважних станів. Такий процес називається рівноважним.

Внутрішньою енергією будь-якого тіла називається енергія цього тіла за вирахуванням кінетичної енергії тіла як цілого і потенційної енергії тіла в зовнішньому полі сил. Наприклад, при визначенні внутрішньої енергії деякої маси газу не повинна враховуватися енергія руху газу разом з посудиною і енергія, обумовлена ​​знаходженням судини в полі сили тяжіння.

Отже, в поняття внутрішньої енергії включаються:

1. кінетична енергія хаотичного руху молекул,
2. потенційна енергія взаємодії між молекулами,
3. внутримолекулярная енергія.

Внутрішня енергія є функцією стану системи. Це означає, що всякий раз, коли система виявляється в даному стані, її внутрішня енергія приймає властиве даному стану значення. Отже, зміна внутрішньої енергії при переході системи з одного стану в інший буде завжди дорівнює різниці значень внутрішньої енергії в цих станах, незалежно від шляху, по якому відбувався перехід.

2.1.3. Перший початок термодинаміки

Внутрішня енергія може змінюватися за рахунок двох процесів: здійснення над тілом роботи А 'і повідомлення йому кількості тепла Q. Наприклад, поршень, всувають в посудину, переміщаючись, здійснює над газом роботу А'. За третім законом Ньютона газ при цьому здійснює над поршнем роботу А = А '.

Повідомлення тілу кількості тепла Q не пов'язане з переміщенням тіл і, отже, не пов'язане з вчиненням над тілом макроскопічної роботи. У цьому випадку зміна внутрішньої енергії обумовлено тим, що окремі молекули більш нагрітого тіла здійснюють роботу над окремими молекулами тіла, нагрітого менш. Сукупність мікроскопічних процесів, що призводять до передачі енергії від тіла до тіла, зветься теплопередачі.

Таким чином, приріст внутрішньої енергії має дорівнювати сумі досконалої над системою роботи і кількості повідомленого системі тепла:

Зазвичай замість роботи зовнішніх сил над системою A 'розглядають роботу А = - A', що здійснюються системою над зовнішніми тілами. Тоді рівняння (2.1.3) можна привести до виду:

Рівняння (2.1.4) виражає закон збереження енергії і є зміст першого початку термодинаміки: кількість тепла, повідомлене системі, йде на приріст внутрішньої енергії системи і на здійснення системою роботи над зовнішніми тілами.

Внутрішню енергію вимірюють, як і роботу, в системі СІ в джоулях. Є також особлива одиниця - 1 калорія, яка дорівнює кількості тепла, необхідного для нагрівання 1 г води від 19,5 до 20,5 ° С. Досвідченим шляхом було встановлено, що 1 кал = 4,18 Дж. Величина I = 4,18 Дж / кал називається механічним еквівалентом тепла.

При обчисленні досконалою системою роботи або отриманого системою тепла доводиться розбивати розглянутий процес на ряд елементарних процесів, кожен з яких відповідає малому зміни параметрів системи. Рівняння (2.1.4) для елементарного процесу має вигляд:

При переході до нескінченно малим величинам рівняння (2.1.5) матиме вигляд:

2.1.4. Робота, що здійснюється тілом
при зміні його об'єму

Взаємодія даного тіла з дотичними з ним тілами можна охарактеризувати тиском. Нехай газ укладений в циліндричний посудину, закритий щільно пригнаний легко ковзає поршнем (Рис. 2.1.2).

Мал. 2.1.2. Робота газу

Якщо газ буде розширюватися, він буде переміщати поршень і здійснювати над ним роботу:

Рівняння (2.1.7) може бути записано так:

При стисненні газу напрямки переміщення і сили, з якою газ діє на поршень, протилежні, внаслідок чого робота буде негативна.

Якщо тиск газу постійно, робота при зміні обсягу дорівнює:

У загальному випадку роботу слід обчислювати так:

Рівняння першого закону термодинаміки для цього випадку можна записати так:

2.1.5. температура

Якщо кілька дотичних тіл знаходяться в стані теплової рівноваги, тобто не обмінюється енергією шляхом теплопередачі, то цим тілам приписується однакова температура. Якщо при встановленні теплового контакту одне з тіл передає іншому енергію, то першому тему приписують температуру, більшу, ніж у другого тіла.

Наведемо тіло, вибране нами для термометричні вимірювань (термометрична тіло), в теплову рівновагу з тающим льодом і пріпішем тілу в цьому випадку температуру 0 ° С. Як термометричні тел вибирають, наприклад, спирт або ртуть. Нехай як ознака зміни температури вибрано зміна обсягу тіла, і значення обсягу, відповідне 0 ° С, позначимо V0. Потім приведемо той же тіло в теплову рівновагу з киплячою при атмосферному тиску водою, пріпішем тілу в цьому випадку температуру 100 ° С, і визначимо відповідний обсяг V100. Беручи, що обсяг змінюється з температурою лінійно, можна стану тіла з довільним об'ємом V приписати температуру:

Встановлена ​​таким чином температурна шкала називається шкалою Цельсія.

2.1.6. Рівняння стану ідеального газу.
Експериментальні газові закони.

Ідеальний газ - це такий газ, внутрішня енергія якого визначається тільки кінетичної енергією складових його молекул. Вважають також, що в цьому випадку обсяг молекул дорівнює нулю. Потенційною енергією взаємодії між молекулами і внутрімолекулярної енергією можна знехтувати за умови, що такий газ має низьку щільність і знаходиться при не дуже високій температурі і тиску. Цій умові зазвичай задовольняють багато гази при нормальних умовах.

Стан деякої маси газу визначається значеннями трьох параметрів: тиску, обсягу і температури. Ці параметри закономірно пов'язані один з одним, так що зміна одного з них тягне за собою зміну інших. Такий зв'язок може бути задана аналітично у вигляді функції:

Співвідношення, подібні (2.1.13), називаються рівняннями стану тіла. Якщо дозволити (2.1.13) щодо будь-якого з параметрів, наприклад р, рівняння стану набуде вигляду:

Наприклад, закон Бойля-Маріотта говорить, що при даній масі газу добуток тиску на об'єм є величина постійна:

Сукупність станів, що відповідають одній і тій же температурі, зображується гіперболою на p - V діаграмі (Рис. 2.1.3).

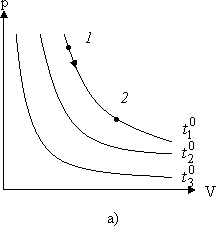
Мал. 2.1.3. Діаграми ізотермічних процесів

Кожному значенню температури відповідає своя крива - ізотерма. При ізотермічному процесі точка, яка зображує стан газу, переміщається по изотерме.

Закон Гей-Люссака говорить, що при постійному тиску об'єм даної маси газу змінюється лінійно з температурою:

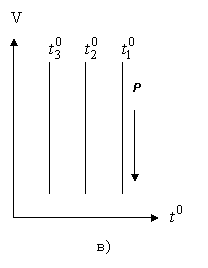
Процес (2.1.16) - изобарических (Рис. 2.1.4а).

Аналогічна залежність є для тиску при постійному обсязі (закон Шарля):

Це - изохорический процес (Рис. 2.1.4б). У рівняннях (2.1.16) і (2.1.17) V0 - об'єм при 0 ° С, р0 - тиск при 0 ° С. коефіцієнт .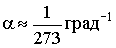

Мал. 2.1.4. Изобарических (а) і изохорический (б) процеси в газах

Все ізобари і ізохори перетинають вісь температур в одній і тій же точці, яка визначається з умови: 1 + αt = 0, звідки випливає:

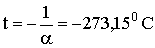
Змістивши початок відліку температур в цю точку, можна перейти від шкали температур за Цельсієм до температурної шкалою Кельвіна, або абсолютної температурної шкали. Відповідно до визначення абсолютної шкали між нею і шкалою Цельсія є співвідношення:

Температура, що дорівнює 0 К, називається абсолютним нулем. Переходячи в співвідношеннях ( 2.1.16 ) І ( 2.1.17 ) До абсолютної температурі, отримаємо:

Використовуючи (2.1.19) і (2.1.20), можна записати:

Газ, який точно слід рівнянням ( 2.1.15 ), (2.1.21) і (2.1.22), називається ідеальним. Всякий реальний газ у напрямку зниження його щільності все більше наближається за властивостями до ідеального газу. Такі гази, як повітря, азот, кисень, при кімнатній температурі і атмосферному тиску дуже близькі до ідеального газу. Особливо близькі за властивостями до ідеального газу гелій і водень.

Об'єднуючи рівняння Бойля-Маріотта і Гей-Люссака, можна знайти рівняння стану ідеального газу. Для цього візьмемо на діаграмі (p, V) два довільних стану, які визначаються параметрами (p1, V1, Т1) і (p2, V2, Т2) (Рис. 2.1.5).

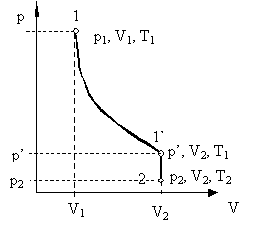
Мал. 2.1.5. До висновку рівняння Клапейрона

Розглянемо перехід з 1 в 2, що складається з ізотерми 1 - 1 'і ізохорами 1' - 2. Стану 1 і 1 'лежать на одній изотерме. Отже, згідно з ( 2.1.15 ), Виконується:

Стану 1 'і 2 лежать на одній Ізохор, тому, згідно з ( 2.1.22 ), Маємо:

Виключаючи з цих рівнянь р ', отримаємо:

Оскільки стану 1 і 2 були взяті довільно, можна стверджувати, що для будь-якого стану буде виконуватися:

Відповідно до закону Авогадро, кілограм-молекули всіх газів займають при однакових умовах однаковий обсяг. При нормальних умовах обсяг одного кіломоля будь-якого газу дорівнює 22,4 м & sup3 / кмоль. Звідси випливає, що в разі, коли кількість газу дорівнює одному кіломолю, величина В в (2.1.26) буде однакова для всіх газів. Позначаючи відповідну кіломолю величину В = R, а обсяг кіломоля через VКМ, рівняння (2.1.26) можна записати у вигляді:

Це рівняння називається рівнянням Клапейрона. Величина R називається універсальною газовою постійною. Її значення можна обчислити, підставляючи в (2.1.27) тиск і температуру при нормальних умовах (1 атм і 273 ° С) і VКМ = 22,4 м & sup3 / кмоль:

Від рівняння для одного кіломоля легко перейти до рівняння для будь-якої маси газу m, взявши до уваги, що при однакових температурі і тиску z кіломолей газу будуть займати в z більший обсяг, ніж один кіломоль: V = zVкм. Помноживши (2.1.27) на z = m / μ (μ - маса кіломоля), отримаємо:

Це і є рівняння стану ідеального газу.

2.1.7. рівняння кінетичної
теорії газів для тиску

Поставимо задачу про обчислення тиску газу на стінки посудини, виходячи з молекулярно-кінетичної моделі газу, згідно з якою газ - це сукупність однакових, хаотичнорухомих, які не взаємодіють один з одним на відстані молекул. Розміри молекул настільки малі, що їх сумарним обсягом можна знехтувати в порівнянні з об'ємом посудини. Вважається, що переважну частину часу молекула рухається вільно, зрідка зазнаючи пружні зіткнення з іншими молекулами або зі стінками посудини. Це - модель ідеального газу.

При ударі об стінку посудини молекула повідомляє їй імпульс, чисельно рівний зміни імпульсу молекули. Всі напрямки руху рівноймовірно, оскільки тиск газу на стінки посудини всюди однаково.

Швидкості молекул можуть бути самими різними і повинні змінюватися при кожному зіткненні, причому вони можуть як зростати, так і зменшуватися. Це випливає з того, що кінетична енергія двох молекул до і після зіткнення повинна бути однакова. Отже, зростання швидкості однієї молекули має супроводжуватися зменшенням швидкості інший.

Введемо деякі спрощення:

1. Нехай молекули рухаються тільки уздовж трьох взаємно перпендикулярних напрямків. Якщо газ містить N молекул, то в будь-який момент часу вздовж кожного з напрямків буде рухатися N / 3 молекул, причому половина з них (N / 6) рухається вздовж даного напряму в одну сторону, половина - в іншу (Рис. 2.1.6) .

   
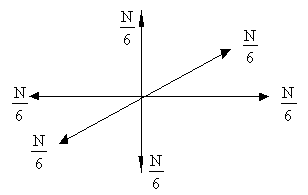
   Мал. 2.1.6. равнораспределенія молекул

   
   

2. Всім молекулам пріпішем однакове значення швидкості v.

   Обчислимо імпульс, який посилає стінки судини вдаряється об неї молекулою. До удару об стінку імпульс молекули спрямований по зовнішньої нормальний до майданчика ΔS і дорівнює за величиною mv (Рис. 2.1.7).

   
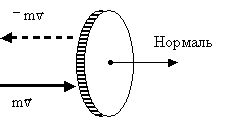
   Мал. 2.1.7. Зміна імпульсу молекули при пружному зіткненні зі стінкою

   
   

   В результаті удару імпульс змінює знак. Таким чином, приріст імпульсу молекули становить:

За третім законом Ньютона стінка отримає при ударі імпульс 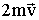, Що має напрямок нормалі. За час Δt до елемента стінки ΔS долетять всі рухомі до нього молекули, укладені в обсязі циліндра з основою ΔS і висотою vΔt. Число цих молекул одно:

Помноживши число ударів (2.1.30) на імпульс (2.1.29), який посилає стінці при кожному ударі, отримаємо сумарний імпульс, який посилає елементу стінки за час Δt:

Відносячи цей імпульс до проміжку часу Δt, отримаємо силу, діючу на елемент стінки:

Ця величина, віднесена до одиниці площі стінки, і є шукане тиск:

З огляду на, що кінетична енергія поступального руху молекули дорівнює 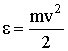, Вираз для тиску набуде вигляду:

Відмовимося зараз від припущення про рівність швидкостей молекул. Нехай n1 молекул мають швидкості, практично рівні v1, n2 молекул мають швидкості, практично рівні v2, ..., і взагалі, ni молекул мають швидкості, практично рівні vi. Очевидно, що виконується:

Знаючи розподіл молекул за швидкостями, можна знайти середнє значення швидкості молекул. Для цього потрібно скласти швидкості всіх молекул і розділити отриманий результат на n:

При записи (2.1.36) враховувалося, що всього є n1 доданків зі швидкістю v1, n2 доданків зі швидкістю v2 і т.д. Провівши аналогічні міркування для кінетичної енергії поступального руху молекул, можна знайти середнє значення їх енергії:

Повторюючи всі міркування для тиску однієї частинки, але замінюючи швидкість на середню швидкість, а кінетичну енергію - на середню кінетичну енергію, формулу для тиску ( 2.1.33 ) Слід записати так:

Рівняння (2.1.38) - це основне рівняння кінетичної теорії газів: тиск дорівнює двом третинам кінетичної енергії поступального руху молекул, укладених в одиниці об'єму.

Температура Т пропорційна тиску ідеального газу при постійному обсязі. З іншого боку, згідно з (2.1.38), тиск пропорційно середньої енергії кінетичного поступального руху молекули. Тому має виконуватися 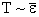. Щоб знайти точне співвідношення, помножимо рівняння (2.1.38) на обсяг кіломоля:

і порівняти (2.1.39) з рівнянням для ідеального газу pVкм = RT. Звідси слідує що:

Отже, абсолютна температура є величина, пропорційна середньої енергії поступального руху однієї молекули. Цей висновок справедливий не тільки для газів, а й для речовини в будь-якому агрегатному стані. Примітно, що середня енергія не залежить від маси молекули.

Замінивши в рівнянні ідеального газу R = NAkБ і враховуючи, що концентрація газу 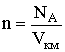отримаємо важливу формулу:

Якщо є суміш декількох газів, різні по масі молекули матимуть різну середню швидкість, але середня енергія молекул буде одна і та ж. Тиск в цьому випадку дорівнюватиме:

Тут n1, n2, і т.д. - концентрації молекул першого, другого і т.д. сорту. Тим самим виявляється, що виконується закон Дальтона: загальний тиск суміші ідеальних газів різного ґатунку дорівнює сумі парціальних тисків газів, що утворюють суміш. Парціальним називають тиск, обумовлене молекулами якого-небудь одного сорту, за умови, що тільки ці молекули присутні в посудині в тій кількості, в якому вони містилися в суміші.

2.1.8. равнораспределенія енергії
за ступенями свободи

В отриманому раніше вираженні:

Числом ступенів свободи механічної системи називається число незалежних координат, що визначають її становище і конфігурацію в просторі.

Так, положення в просторі МТ (частки газу, що складається з атомів одного сорту) може бути повністю задано трьома координатами. Уявімо енергію поступального руху такої частки у вигляді суми трьох доданків - кінетичних енергій руху молекули за трьома взаємно перпендикулярним напрямам:

Повна хаотичність руху молекули дозволяє вважати, що середні значення кінетичних енергій за трьома напрямками рівні один одному:

Зіставляючи (2.1.43) і (2.1.45), отримуємо, що на одну ступінь поступального руху матеріальної точки доводиться енергія, рівна:

Якби, наприклад, існував такий гіпотетичний одноатомний "одновимірний" газ, всі частинки якого мали б здатністю рухатися тільки вздовж однієї прямої, то середня кінетична енергія молекули такого газу дорівнювала б .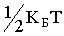

Природно припустити, що якби молекула газу мала б ще якимись ступенями свободи, то і на кожну з них припадає середнє значення кінетичної енергії, рівне 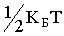. У класичній статистичній фізиці Л. Больцманом доведена теорема: якщо система молекул знаходиться в тепловій рівновазі при температурі Т, то середня кінетична енергія рівномірно розподілена між усіма ступенями свободи і для кожного ступеня свободи молекули вона дорівнює 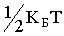. Ця теорема називається законом рівномірного розподілу кінетичної енергії за ступенями свободи.

Відносно своєї внутрішньої енергії дво- і багатоатомні гази відрізняються від одноатомних числом ступенів свободи своїх молекул. Отже, для обчислення внутрішньої енергії газу треба вміти визначати число ступенів свободи.

Розглянемо найпростіший випадок двоатомних молекули (Н2, О2, N2, CO, NO, ...) (Рис. 2.1.8).

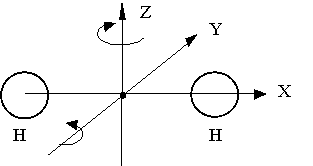
Мал. 2.1.8. Модель двоатомних молекули

Якщо відстань між атомами не змінюється (такі молекули називаються жорсткими), то така система, в загальному випадку, буде мати шість ступенів свободи. Дійсно, положення і конфігурація такої молекули визначається: трьома координатами її центру мас, які задають поступальний рух молекули як цілого, і трьома координатами, що визначають можливі обертання молекули навколо кожної з трьох осей X, Y, Z.

Однак досвід і теорія показують, що обертання таких молекул навколо осі Х, на якій лежать центри атомів, може бути порушено лише при високих температурах. При звичайних температурах обертання навколо цієї осі не відбувається. Це можна також пояснить тією обставиною, що при обертанні навколо даної осі момент інерції молекули - найменший, і енергетичний вклад від такого руху повинен бути мінімальним.

Отже, число ступенів свободи жорсткої двоатомних молекули дорівнює 5: 3 - поступальних + 2 - обертальних.

Атоми і молекули не завжди жорстко пов'язані один з одним, вони можуть здійснювати коливання відносно один одного. Тоді буде потрібно ще одна координата для визначення конфігурації молекули - відстань між атомами.

Таким чином, для двоатомних молекули з пружним зв'язком між атомами існує 6 ступенів свободи: 3 - поступальних + 2 - обертальних + 1 - коливальна. У багатьох випадках коливальні рухи атомів не порушуються. Але якщо вони існують, і якщо їх амплітуди малі в порівнянні з відстанню між атомами, то такі коливання можна вважати гармонійними. Атоми в цьому випадку є гармонійними осцилляторами. Однак осцилятор має не тільки кінетичної, а й потенційну енергію. Для гармонічного осцилятора, як відомо з механіки, середні значення кінетичної і потенційної енергії рівні між собою. Отже, якщо порушені гармонійні коливання атомів, то згідно із законом равнораспределенія на кожну коливальну ступінь свободи молекули припадає 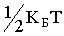у вигляді кінетичної енергії і 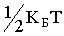у вигляді потенційної енергії. Тому енергія, що припадає на одну коливальну ступінь свободи молекули, дорівнює kБТ.

Якщо молекула складається з n атомів, які не жорстко пов'язаних, то вона має 3n ступенів свободи (кожен атом має 3 ступеня свободи). З цього числа 3 - поступальних + 3 - обертальних, за винятком випадку, коли атоми розташовані на одній прямій, - тоді обертальних ступенів свободи - 2 (як у двоатомних молекули).

На Рис. 2.1.9 приведена модель трехатомного молекули.

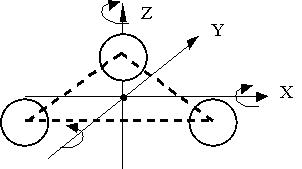
Мал. 2.1.9. Модель трехатомного молекули

Таким чином, нелінійна n - атомна молекула в загальному випадку може мати (3n - 6) коливальних ступенів свободи, а лінійна - (3n - 5).

Таким чином, середня енергія молекули повинна дорівнювати:

Для молекул з жорсткою зв'язком між атомами i збігається з числом ступенів свободи молекули.

2.1.9. Внутрішня енергія
і теплоємність ідеального газу

Внаслідок того, що молекули ідеального газу не взаємодіють на відстані, внутрішня енергія такого газу складається з енергій окремих молекул. Отже, внутрішня енергія одного кіломоля ідеального газу буде дорівнює добутку числа Авогадро на середню енергію однієї молекули:

Внутрішня енергія довільної маси газу m дорівнюватиме внутрішньої енергії одного моля, помноженої на число кіломолей газу, що містяться в масі m:

Теплоємністю будь-якого тіла називається кількість тепла, яке потрібно повідомити тілу, щоб підвищити його температуру на один градус:

Теплоємність одного кіломоля позначається літерою С та має розмірність Дж / град · кмоль. Теплоємність з одиниці маси називається питомою теплоємністю і має розмірність Дж / град · кг. Між питомою теплоємністю і теплоємністю одного кіломоля є очевидне співвідношення:

Величина теплоємності залежить від умов, при яких відбувається нагрівання тіла. Найбільший інтерес представляють два випадки:

1. нагрівання тіла виробляється при постійному обсязі (СV);
2. нагрівання тіла виробляється при постійному тиску (Ср).

Якщо нагрівання тіла виробляється при постійному обсязі, тіло не робить роботи над зовнішніми тілами і, згідно першому початку термодинаміки ( 2.1.11 ), Все тепло йде на приріст внутрішньої енергії тіла:

З (2.1.53) випливає, що теплоємність будь-якого тіла при постійному обсязі дорівнює:

Підставляючи в (2.1.54) співвідношення ( 2.1.49 ), Отримаємо вираз для теплоємності кіло-моля ідеального газу:

Звідси випливає, що теплоємність кіломоля ідеального газу, виміряна при постійному обсязі, не залежить від параметрів стану газу. Виходячи з (2.1.55), в цьому випадку можна уявити внутрішню енергію так:

Якщо нагрівання тіла виробляється при постійному тиску, то газ буде розширюватися, здійснюючи над зовнішніми тілами позитивну роботу. Отже, для підвищення температури газу на один градус в цьому випадку буде потрібно більше тепла, ніж при нагріванні при постійному обсязі, - частина тепла буде витрачена на вчинення газом роботи.

Напишемо рівняння першого початку термодинаміки ( 2.1.11 ) Для кіломоля газу:

Розділивши (2.1.57) на dT, отримаємо, з урахуванням (2.1.54), вираз для теплоємності кіло моля ідеального газу при постійному тиску:

Відповідно до рівняння стану ідеального газу ( 2.1.27 ) 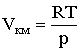і за допомогою (2.1.58), маємо:

Таким чином, робота, яку здійснює кіломоль ідеального газу при підвищенні його температури на один градус при постійному тиску, виявляється рівною універсальної газової постійної. З урахуванням формули ( 2.1.55 ) Співвідношення (2.1.59) набуде вигляду:

Поділивши (2.1.60) на ( 2.1.55 ), Знайдемо характерне для кожного газу відношення γ = Ср / СV:

У Табл. 2.1.1 наводяться значення Ср, CV і γ для різних молекул, в Табл. 2.1.2 зіставлені результати теорії з експериментом. Теоретичні значення отримані в припущенні, що молекули є жорсткими, експериментальні дані наводяться для температур, близьких до кімнатних.

Таблиця 2.1.1

Таблиця 2.1.2

Порівняння експериментальних і
теоретичних властивостей деяких газів Газ Кількість
атомів в
молекулі СV, 10 & sup3 Дж / град · кмоль Сp, 10 & sup3 Дж / град · кмоль γ теор. експ. теор. експ. теор. експ. Гелій (Не) 1 12,5 12,5 20,8 20,9 1,67 1,67 Кисень (О2) 2 20,8 20,9 29,1 28,9 1,40 1,40 Окис вуглецю (СО ) 2 20,8 21,0 29,1 29,3 1,40 1,40 Пари води (Н2О) 3 25,0
33,2 *) 27,8 33,2
41,5 *) 36,2 1,33
1,25 *) 1,31

*) Для i = 8, тобто в припущенні, що є додатково одна коливальна ступінь свободи.

Відповідно до класичної теорії, теплоємність не повинна залежати від температури. Однак на Рис. 2.1.10 така залежність для молекул водню існує.

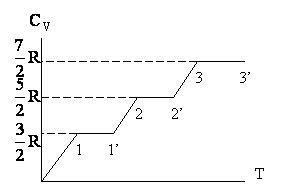
Мал. 2.1.10. Температурна залежність теплоємності водню

Немає температурної залежності тільки в певних температурних областях, причому в таких областях теплоємність має значення, відповідні різному числу ступенів свободи молекули. Так, на ділянці 1 - 1 'СV = 3 / 2R, що означає, що молекула веде себе як система, що володіє тільки поступальними ступенями свободи. На ділянці 2 - 2 'СV = 5 / 2R, отже, при температурах, які відповідають цій інтервалу, у молекули, на додаток до виявляється при більш низьких температурах трьом поступальним ступеням свободи, додаються ще дві обертальні. Нарешті, при досить високих температурах Cv = 7 / 2R, що свідчить про наявність при цих температурах коливання в молекулі. У проміжку між названими інтервалами теплоємність з температурою монотонно зростає, що говорить про те, що в новий вид руху залучаються не всі молекули відразу. Причини такої поведінки можуть бути пояснені тільки на основі квантово-підходу.

2.1.10. Рівняння адіабати ідеального газу

Адіабатичним називається такий процес, який протікає без теплообміну з навколишнім середовищем. Для його опису підставимо в рівняння першого початку термодинаміки ( 2.1.11 ) Вираз для внутрішньої енергії ( 2.1.58 ), Узяте для ідеального газу з масою m:

Так як для адіабатичного процесу δQ = 0, то має виконуватися:

Використовуючи рівняння стану ідеального газу, отримаємо 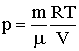. Підставляючи цей вираз в (2.1.63), після перетворення маємо:

Дане співвідношення можна представити так:

з ( 2.1.59 ) Слід, що Ср - СV = R. Тому, вводячи величину

Це - рівняння адіабати ідеального газу в змінних Т і V. Від цього рівняння можна перейти до рівняння в змінних p і V, використовуючи рівняння стану ідеального газу в вигляді 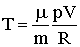. Тоді рівняння (2.1.68) можна записати:

Це - рівняння адіабати ідеального газу в змінних p і V, зване також рівнянням Пуассона.

У всіх міркуваннях передбачалося, що стан ідеального газу в кожен момент часу характеризується певними значеннями параметрів p і Т, тобто що даний процес є рівноважним. Однак рівноважним може бути процес, що протікає дуже повільно. Разом з тим, оскільки в природі не існує абсолютно не проводять тепло речовин, кількість тепла, яким система обмінюється зі своїм оточенням, буде тим менше, ніж менший час триває процес. Отже, близькими до адиабатическим можуть бути тільки швидко протікають процеси, наприклад, стиснення і розширення газу при поширенні через нього звукової хвилі.

2.1.11. политропического процеси

Усі розглянуті раніше процеси - це окремі випадки политропического процесу. Политропического називається такий процес, при якому тиск і обсяг ідеального газу пов'язані співвідношенням:

Таблиця 2.1.3

Политропического процеси n Процес n Процес 0 изобарического γ Адіабатичний 1 Ізотермічний ± ∞ Ізохоричний

Перші три рядки очевидні. Щоб переконатися в справедливості четвертого рядка, запишемо рівняння політропи (2.1.70) для двох довільних станів:

Винесемо з (2.1.71) корінь n - ступеня:

Спрямовуючи n → ± ∞, прийдемо до умови:

2.1.12. барометрична формула

Атмосферний тиск на будь-якої висоті h обумовлено вагою верхніх шарів газу. Нехай на цій висоті тиск одно р. Тоді тиск на висоті h + dh одно р + dp, причому якщо dh> 0, то dp <0, так як вага верхніх шарів атмосфери, а, отже, і тиск з висотою убувають. Різниця тисків р і р + dp дорівнює вазі газу, укладеного в обсязі циліндра з площею основи, що дорівнює одиниці, і висотою dh (Рис. 2.1.11):

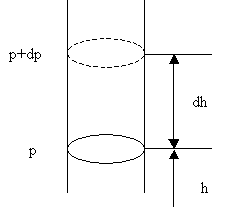
Мал. 2.1.11. До висновку барометрической формули

Звідси випливає:

За умов, близьких до нормальних, гази, що входять до складу атмосфери, мало відрізняються за своїми властивостями від ідеального газу. Тому, використовуючи рівняння стану ідеального газу, для щільності газу можна записати:

Підставляючи (2.1.76) в (2.1.75), отримаємо:

Для випадку, коли температура постійна, інтегруючи (2.1.78), отримаємо:

Потенціюючи (2.1.79) маємо співвідношення:

Нехай при h = 0 виконується р = р0. Використовуючи цю умову, з (2.1.80) отримаємо: р (h = 0) = р0 = C. Остаточне вираз для залежності атмосферного тиску газу від висоти при даній температурі набуде вигляду:

Ця формула називається барометричної. З неї випливає, що тиск зменшується з висотою тим швидше, чим важче газ (чим більше μ) і чим нижче температура (Рис. 2.1.12).

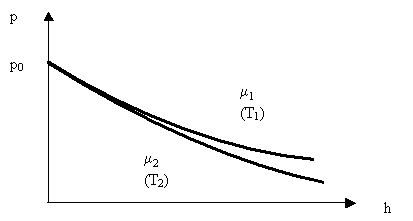
Мал. 2.1.12. Залежність тиску газу від висоти і температури (μ1 <μ2, Т1> Т2)

2.1.13. РозподілБольцмана

Замінивши в (2.1.81) тиск р = nkБТ, отримаємо закон зміни концентрації газу в залежності від висоти:

Тут n0 - число молекул в одиниці об'єму на висоті, що дорівнює нулю, n - їх концентрація на висоті h. Перетворимо (2.1.82), використовуючи зв'язок :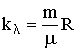

З (2.1.83) випливає, що зі зниженням температури число частинок на висотах, відмінних від нуля, убуває, звертаючись в нуль при T = 0 (Рис. 2.1.13).

Мал. 2.1.13. Зміна концентрації частинок газу з висотою

При абсолютному нулі всі молекули розташувалися б на поверхні землі. При високих температурах, навпаки, концентрація частинок слабо зменшується з висотою, так що молекули виявляються розподілені по висоті майже рівномірно.

Дійсно, кожне конкретне розподіл молекул по висоті встановлюється в результаті спільного і конкуруючої дії двох чинників:

1. тяжіння молекул до Землі прагне розташувати їх на поверхні;
2. тепловий рух перешкоджає цьому і прагне розподілити молекули по висоті рівномірно.

Чим більше маса і менше температура, тим сильніше переважає перший фактор, і молекули виявляться сконцентровані ближче до Землі. Наприклад, молекули важкого газу радону можуть накопичуватися в підвалах будинків.

На різній висоті молекула з масою m володіє різним запасом потенційної енергії:

Тому формулу ( 2.1.83 ) Можна представити так:

Л.Больцман довів, що розподіл (2.1.85) справедливо не тільки в разі поля сили тяжіння, а й в будь-якому потенційному полі сил для сукупності будь-яких однакових часток, що знаходяться в стані хаотичного теплового руху. Формулу (2.1.85) називають розподілом Больцмана.